publications

2024

1. A Moral Imperative: The Need for Continual Superalignment of Large Language Models

   Gokul Puthumanaillam^*, Manav Vora^*, Pranay Thangeda, and Melkior Ornik

   arXiv preprint arXiv:2403.14683, 2024

   Abs PDF

   

   This paper examines the challenges associated with achieving life-long superalignment in AI systems, particularly large language models (LLMs). Superalignment is a theoretical framework that aspires to ensure that superintelligent AI systems act in accordance with human values and goals. Despite its promising vision, we argue that achieving superalignment requires substantial changes in the current LLM architectures due to their inherent limitations in comprehending and adapting to the dynamic nature of these human ethics and evolving global scenarios. We dissect the challenges of encoding an ever-changing spectrum of human values into LLMs, highlighting the discrepancies between static AI models and the dynamic nature of human societies. To illustrate these challenges, we analyze two distinct examples: one demonstrates a qualitative shift in human values, while the other presents a quantifiable change. Through these examples, we illustrate how LLMs, constrained by their training data, fail to align with contemporary human values and scenarios. The paper concludes by exploring potential strategies to address and possibly mitigate these alignment discrepancies, suggesting a path forward in the pursuit of more adaptable and responsive AI systems.

2. 

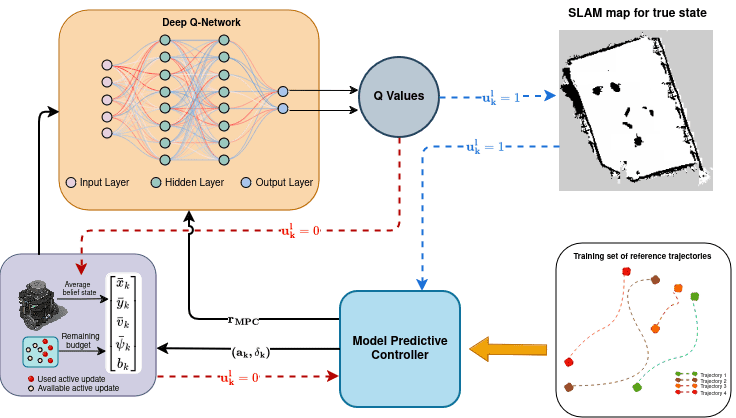   ComTraQ-MPC: Meta-Trained DQN-MPC Integration for Trajectory Tracking with Limited Active Localization Updates

   Gokul Puthumanaillam^*, Manav Vora^*, and Melkior Ornik

   In 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2024

   Abs DOI PDF Video Code

   

   Optimal decision-making for trajectory tracking in partially observable, stochastic environments where the number of active localization updates – the process by which the agent obtains its true state information from the sensors – are limited, presents a significant challenge. Traditional methods often struggle to balance resource conservation, accurate state estimation and precise tracking, resulting in suboptimal performance. This problem is particularly pronounced in environments with large action spaces, where the need for frequent, accurate state data is paramount, yet the capacity for active localization updates is restricted by external limitations. This paper introduces ComTraQ-MPC, a novel framework that combines Deep Q-Networks (DQN) and Model Predictive Control (MPC) to optimize trajectory tracking with constrained active localization updates. The meta-trained DQN ensures adaptive active localization scheduling, while the MPC leverages available state information to improve tracking. The central contribution of this work is their reciprocal interaction: DQN’s update decisions inform MPC’s control strategy, and MPC’s outcomes refine DQN’s learning, creating a cohesive, adaptive system. Empirical evaluations in simulated and real-world settings demonstrate that ComTraQ-MPC significantly enhances operational efficiency and accuracy, providing a generalizable and approximately optimal solution for trajectory tracking in complex partially observable environments.

3. 

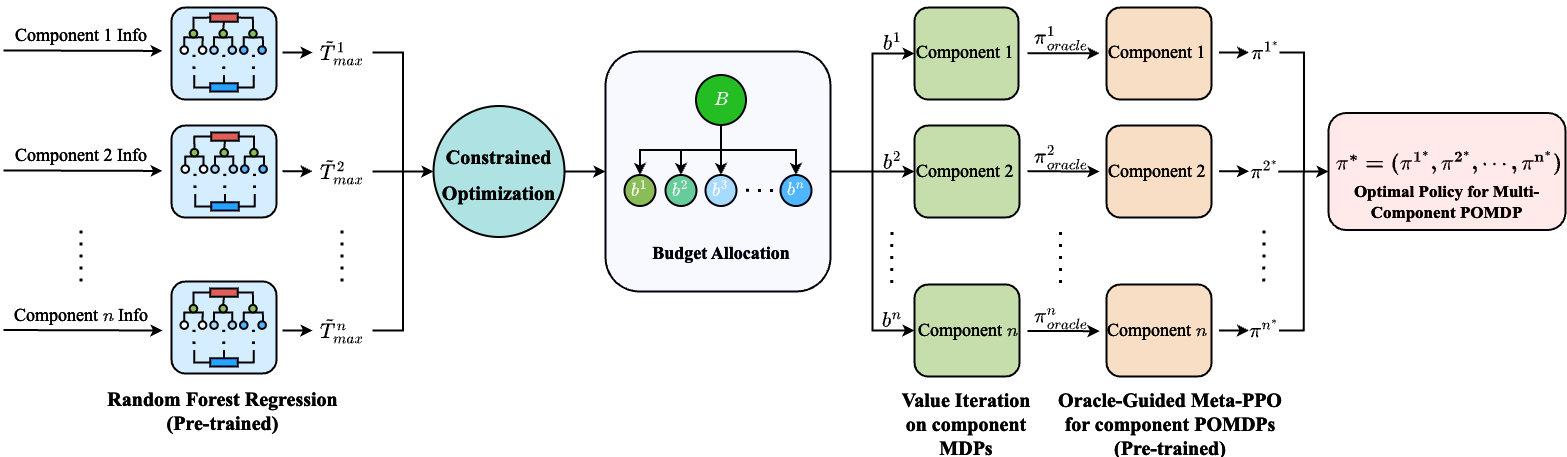   Solving Truly Massive Budgeted Monotonic POMDPs with Oracle-Guided Meta-Reinforcement Learning

   Manav Vora, Michael N Grussing, and Melkior Ornik

   arXiv preprint arXiv:2408.07192, 2024

   Abs PDF

   

   Monotonic Partially Observable Markov Decision Processes (POMDPs), where the system state progressively decreases until a restorative action is performed, can be used to model sequential repair problems effectively. This paper considers the problem of solving budget-constrained multi-component monotonic POMDPs, where a finite budget limits the max imal number of restorative actions. For a large number of components, solving such a POMDP using current methods is computationally intractable due to the exponential growth in the state space with an increasing number of components. To address this challenge, we propose a two-step approach. Since the individual components of a budget-constrained multi-component monotonic POMDP are only connected via the shared budget, we first approximate the optimal budget allocation among these components using an approximation of each component POMDP’s optimal value function which is obtained through a random forest model. Subsequently, we introduce an oracle-guided meta-trained Proximal Policy Op timization (PPO) algorithm to solve each of the independent budget-constrained single-component monotonic POMDPs. The oracle policy is obtained by performing value iteration on the corresponding monotonic Markov Decision Process (MDP). This two-step method provides scalability in solv ing truly massive multi-component monotonic POMDPs. To demonstrate the efficacy of our approach, we consider a real world maintenance scenario that involves inspection and re pair of an administrative building by a team of agents within a maintenance budget. Our results show that the proposed method significantly improves average component survival times compared to baseline policies, thereby highlighting its potential for practical applications in large-scale maintenance problems. Finally, we perform a computational complexity analysis for a varying number of components to show the scalability of the proposed approach.

4. 

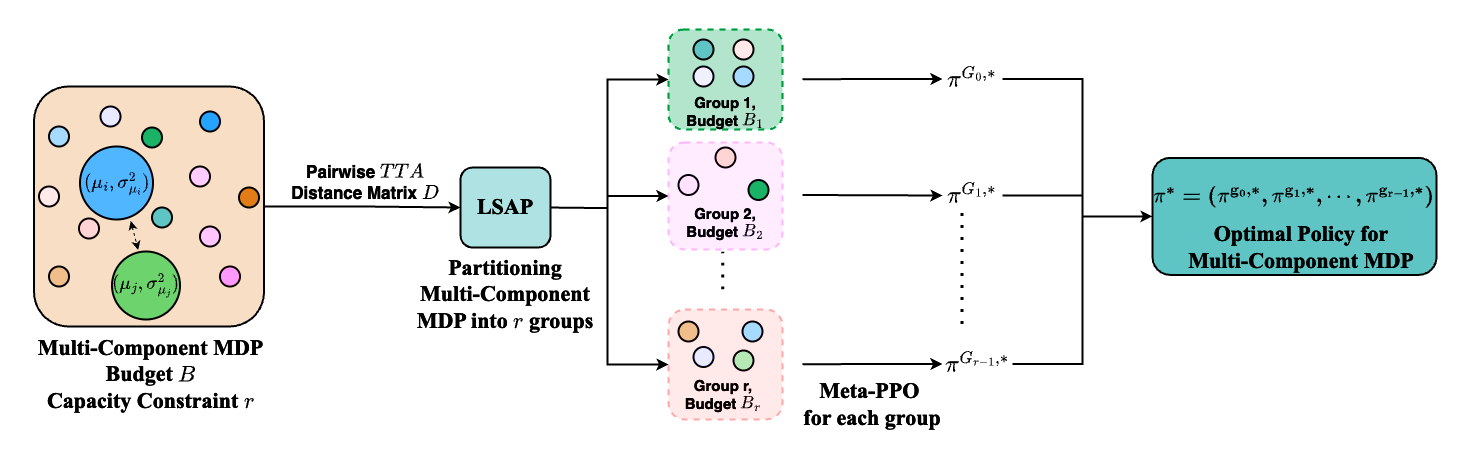   Capacity-Aware Planning and Scheduling in Budget-Constrained Monotonic MDPs: A Meta-RL Approach

   Manav Vora, Ilan Shomorony, and Melkior Ornik

   arXiv preprint arXiv:2410.21249, 2024

   Abs PDF

   

   Many real-world sequential repair problems can be effec tively modeled using monotonic Markov Decision Processes (MDPs), where the system state stochastically decreases and can only be increased by performing a restorative action. This work addresses the problem of solving multi-component monotonic MDPs with both budget and capacity constraints. The budget constraint limits the total number of restora tive actions and the capacity constraint limits the number of restorative actions that can be performed simultaneously. While prior methods dealt with budget constraints, capacity constraints introduce an additional complexity in the multi component action space that results in a combinatorial op timization problem. Including capacity constraints in prior methods leads to an exponential increase in computational complexity as the number of components in the MDP grows. We propose a two-step planning approach to address this challenge. First, we partition the components of the multi component MDP into groups, where the number of groups is determined by the capacity constraint. We achieve this partitioning by solving a Linear Sum Assignment Problem (LSAP), which groups components to maximize the diversity in the properties of their transition probabilities. Each group is then allocated a fraction of the total budget proportional to its size. This partitioning effectively decouples the large multi-component MDP into smaller subproblems, which are computationally feasible because the capacity constraint is simplified and the budget constraint can be addressed us ing existing methods. Subsequently, we use a meta-trained PPOagenttoobtain an approximately optimal policy for each group. To validate our approach, we apply it to the problem of scheduling repairs for a large group of industrial robots, constrained by a limited number of repair technicians and a total repair budget. Our results demonstrate that the proposed method outperforms baseline approaches in terms of maxi mizing the average uptime of the robot swarm, particularly for large swarm sizes. Lastly, we confirm the scalability of our approach through a computational complexity analysis across varying numbers of robots and repair technicians.

5. 

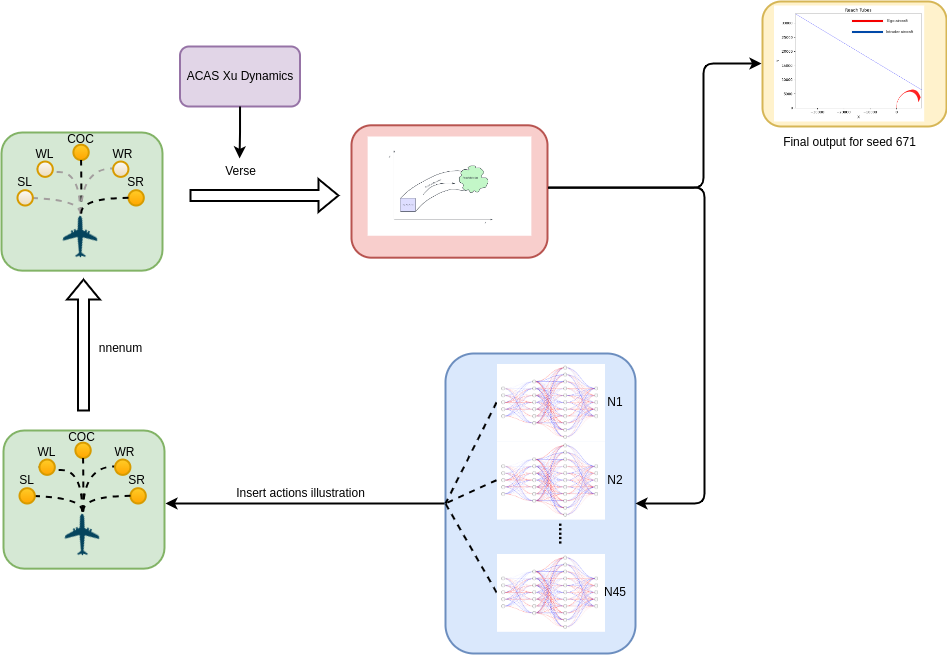   Assured Collision Avoidance for Learned Controllers: A Case Study of ACAS Xu

   Gokul Puthumanaillam^*, Manav Ketan Vora^*, Taha Shafa, Yangge Li, Melkior Ornik, and Sayan Mitra

   In AIAA SCITECH 2024 Forum, 2024

   Abs PDF

   

   This paper introduces a novel approach to verification of neural network controlled systems, combiningthecapabilities of the nnenumframeworkwiththeVersetoolkit. Addressingacritical gap in the traditional verification process which often does not include the system dynamics analysis while computing the neural network outputs, our integrated methodology enhances the precision and safety of decision-making in complex dynamical systems. By iteratively verifying neural network decisions and propagating system states, we maintain an accurate representation of the system’s behavior over time, a vital aspect in ensuring operational safety. Our approach is exemplified through the verification of the neural network controlled Airborne Collision Avoidance System for Unmanned Aircraft (ACAS Xu). We demonstrate that the integration of nnenum and Verse not only accurately computes reachable sets for the UAS but also effectively handles the inherent complexity and nonlinearity of the system. The resulting analysis provides a nuanced understanding of the system’s behavior under varying operational conditions and interactions with other agents, such as intruder aircraft. The comprehensive simulations conducted as part of this study reveal the robustness of our approach, validating its effectiveness in verifying the safety and reliability of learned controllers. Furthermore, the scalability and adaptability of our methodology suggest its broader applicability in various autonomous systems requiring rigorous safety verification.

2023

1. 

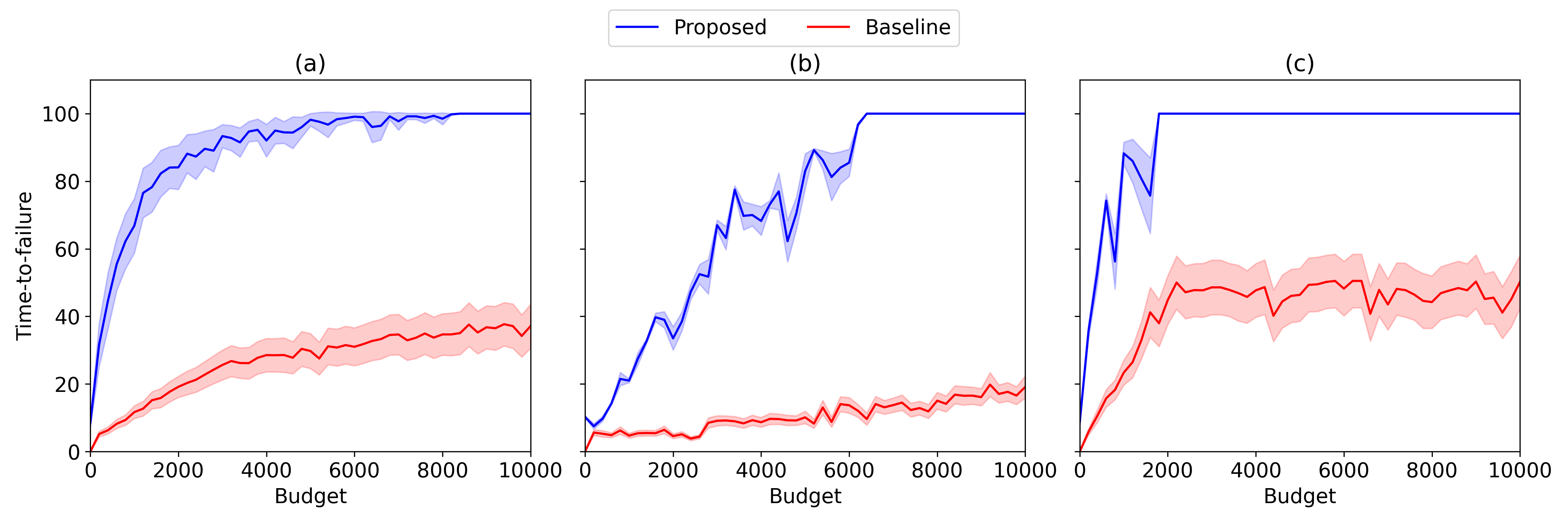   Welfare Maximization Algorithm for Solving Budget-Constrained Multi-Component POMDPs

   Manav Vora, Pranay Thangeda, Michael N Grussing, and Melkior Ornik

   IEEE Control Systems Letters, 2023

   Abs PDF

   

   Partially Observable Markov Decision Processes (POMDPs) provide an efficient way to model real-world se- quential decision making processes. Motivated by the problem of maintenance and inspection of a group of infrastructure components with independent dynamics, this paper presents an algorithm to find the optimal policy for a multi-component budget-constrained POMDP. We first introduce a budgeted- POMDP model (b-POMDP) which enables us to find the optimal policy for a POMDP while adhering to budget constraints. Next, we prove that the value function or maximal collected reward for a special class of b-POMDPs is a concave function of the budget for the finite horizon case. Our second contribution is an algorithm to calculate the optimal policy for a multi- component budget-constrained POMDP by finding the optimal budget split among the individual component POMDPs. The optimal budget split is posed as a welfare maximization problem and the solution is computed by exploiting the concavity of the value function. We illustrate the effectiveness of the proposed algorithm by proposing a maintenance and inspection policy for a group of real-world infrastructure components with different deterioration dynamics, inspection and maintenance costs. We show that the proposed algorithm vastly outperforms the policies currently used in practice.